&nbap;

오랜만에 영화를 봤네..ㅋㅋ

수학과 접목시킨 긴장감있는 영화였다..
(그 정신에 그 문제들을 풀수 있다니 대다나다~)

암튼 영화에서 나왔던 문제들이 호기심이 생겨서 찾아보니 깨알같은 정보들이 많이 있다..ㅋ

먼저 영화 전체에 나오는 현대수학의 영원한 난제, 골드바흐의 정의!!

1742년 수학자 크리스찬 골드바흐는 모든 짝수는 두개의 소수를 합한 숫자라는 걸 알아냈다.

모든 짝수는 두 소수의 합이다.
– C. 골드바흐

골드바흐는 당시 최고의 수학자였던 오일러에게 자신이 알아낸 것이 일반적인 것인지에 대해 묻는다.

오일러는 골드바흐의 질문은 둘로 나누어 정리한다.

정리1. 2보다 큰 짝수는 두 소수의 합으로 나타낼 수 있다
정리2. 5보다 큰 홀수는 세 소수의 합으로 나타낼 수 있다

정리2는 1937년 러시아의 ‘이반 비노그라도프’가 증명했다.
남아있는 건 정리1.. 이건 ‘골드바흐의 추측’이라고 불려진다.

아직까지도 골드바흐의 추측은 증명되지 않은 채 난제로 남아있다.

그리고 초대를 위해 사용된 문제..

5-4-2-9-8-6-7-3-1 숫자 패턴을 구하라.

[풀이]
각 숫자에 대한 스페인어 명칭은 다음과 같다.
1 : uno , 2 : dos , 3 : tres , 4 : cuatro , 5 : cinco , 6 : seis , 7 : siete , 8 : ocho , 9 : nueve
각 숫자의 명칭에 있는 알파벳 순서로 숫자들을 나열해 보면 다음과 같습니다.
5(cinco) – 4(cuatro) – 2(dos) – 9(nueve) – 8(ocho) – 6(seis) – 7(siete) – 3(tres) – 1(uno)

배를 타고 건너면서 할아버지가 낸 문제..(너무나 많이 알려져서 유명한..)

양치기가 양/늑대/양배추와 함께 강을 건너야 한다.
양과 늑대를 남겨두면 늑대가 양을 잡아먹고, 양과 양배추를 남겨두면 양이 양배추를 먹는다.
전부 다 무사히 가지고 가려면 어떻게 해야 할까? (한번에 하나의 물건만 가지고 강을 건널 수 있다.)

[풀이]
맨 처음 양을 데리고 강을 건넌 다음 양만 강 건너편에 두고 돌아온다.
그 다음 양배추를 가지고 강을 건너 양배추를 높은 뒤 양은 다시 데리고 온다.
세 번째로 강을 건널 때에는 늑대를 데리고 가서 건너편에 늑대와 양배추를 함께 있게 한다.
양치기가 양과 함께 마지막으로 강을 건너오면 모든 일행이 강은 건너가게 된다.

페르마의 밀실에서 첫번째 문제..

과자 가게 주인이 속이 보이지 않는 상자 세 개를 받았다. 한 상자에는 박하사탕이, 다른 상자에는 아니스 사탕이,
그리고 나머지 하나에는 박하사탕과 아니스 사탕이 섞여 들어있다. 각 상자에는 박하, 하니스, 혼합이라는 라벨리 하나씩 붙어있지만
모두 잘못되었다고 한다. 상자 속의 내용물들을 정확히 알기 위해서는 최소한 몇번 사탕상자를 확인해야 하는가?

[풀이]
1번
라벨이 제대로 붙여져 있는 상자는 하나도 없다는 것이 중요하다. ‘혼합’ 이라는 라벨이 붙여진 상자를 열어 내용물을 확인한다.
‘혼합’ 라벨이 붙었으므로 그 상자는 박하사탕과 아니스사탕이 혼합된 것이 아니므로 박하사탕과 나오면
박하사탕 상자가 된다(아니스 사탕이 나오면 아니스 사탕 상자인 것이다.) 그리고 남은 상자는 아니스 상자와 혼합 상자인데,
박하사탕 상자는 이미 나왔으므로 ‘아니스’라는 라벨이 붙은 상자는 혼합, ‘박하’ 라는 라벨이 붙은 상자는 자동으로 아니스 사탕 상자임

페르마의 밀실에서 두번째 문제..

아래의 코드를 해독하시오.
00000000000000011111111100011111111111001111111111100110001000110011000100011001111101111100111110111110
00111111111000001010101000000110101100000011111110000000000000000

[풀이]
169개의 코드! 13*13 이므로 배열로 생각하여 0이면 민무늬, 1이면 도형 으로 블럭을 생각하면 아래 그림이 나온다.

페르마의 밀실에서 세번째 문제..

밀폐된 방 안에 전등이 하나 있다. 방 밖에는 3개의 스위치가 있다. 스위치 셋 중 하나만이 전등을 켤 수 있다.
문이 답혀있는 동안에는 스위치를 마음대로 누를 수 있지만, 문을 열었을 때는 스위치 셋 중 어느 것이 전들을 켜는지 말해야한다.

[풀이]
1번 스위치를 오랜 시간 동안 켜 높는다. 그런 다음 1번 스위치를 끄고 2번 스위치를 켠 다음 방문을 열어 전들을 만져본다.
전등이 뜨겁고 불이 꺼졌다면 답은 1번 스위치이다.
전등이 차갑고 불이 껴졌다면 답은 2번 스위치이다.
전등이 차갑고 불이 꺼졌다면 답은 3번 스위치이다.

페르마의 밀실에서 네번째 문제..

9분의 시간을 재야할 때 4분과 7분의 모래시계로 재는 방법은 무엇인가?

[풀이]
4분 모래시계를 4, 7분 모래시계를 7이라 하자.
우선 4와 7을 동시에 뒤집는다. 4의 모래가 모두 떨어지면 4를 다시 뒤집는다.
7의 모래가 모두 떨어지면 7도 역시 다시 뒤집어 준다.
또 다시 4의 모래가 모두 떨어지면 7을 다시 뒤집어 준다.
7의 모래가 모두 떨어졌을 때가 바로 9분이 지났을 때이다.

페르마의 밀실에서 다섯번째 문제..

한 학생이 선생님께 물었다. “따님 세분의 나이가 몇 살인가요?”
선생님이 대답하길, “곱하기를 하면 36이고, 더하기를 하면 너희 집주소다”
설명이 바졌다고 학생이 되묻자 선생님은 “그렇구나 제일 큰 아이는 피아노를 친다” 라고 대답했다.
딸 세 명의 나이는 몇 살인가?

[풀이]
9살, 2살, 2살
곱하기를 해서 36이 나오는 세 개의 숫자와 그 숫자들의 합은 다음과 같다.
(1,1,36) (1,2,18) (1,3,12) (1,4,9) (1,6,6) (2,2,9) (2,3,6) ==> 38, 21, 16, 14, 13, 13, 11
학생이 곱하기와 더하기에 대한 이야기를 듣고 자신의 집 주소만 찾으면 되었는데도 설명이 빠졌다고 한 것은 더해서 자기의 집 주소가 되는 숫자가 하나 넘게 있다는 뜻이다. (1, 6, 6)과 (2, 2, 9)는 더해서 13이 된다.
그런데 문제에서 선생님이 “제일 큰 아이” 라고 했으므로 첫째 딸과 둘째 달은 나이 차이가 있다는 얘기가 된다.
답이 (1, 6, 6) 인 경우는 제일 나이가 많은 아이가 두명이 되므로 맞지 않는다. 그러므로 답은 (2, 2, 9) 가 된다.

페르마의 밀실에서 여섯번째 문제..

거짓의 나라에선 사람들이 다 거짓말을 하고, 진실의 나라에선 사람들이 다 진실을 말한다.
한 외국인이 문이 둘 있는 방에 갇혔다. 문 하나는 자유로 가는 길이고, 다른 문은 아니다.
한 문은 거짓나라의 간수가, 다른 한 문은 진실나라의 간수가 지키고 있다. 외국인은 자유를 얻기 위해
한 간수에게 한 번 질문을 해 답을 들을 수 있다. 어느 쪽이 진실나라 사람이고 어느 쪽이 거짓나라 사람인지 알 수 없다.
이 경우, 외국인은 어떤 질문을 해야 하는가?

[풀이]
간수에게 “저 간수는 어느 쪽 문이 자유로 가는 문이라고 할 것 같은가” 라고 물어보고 두 간수가 말한 문과 다른 문을 선택하면 됨.

거짓 나라의 간수는 진실나라의 간수가 자유로 가는 문을 제대로 가리킨다는 것을 아니까 자유가 아닌 문을 말할 것이고,
진실나라의 간수는 거짓나라의 간수가 거짓으로말할 것을 알기 때문에 역시 자유가 아닌 문을 말하게 될 것이다.
외국인은 두 간수가 가리킨 문이 아닌 다른 문을 선택하면 된다.

페르마의 밀실에서 일곱번째 문제..

어머니는 아들보다 21살이 많다. 6년 안에 아들은 어머니보다 5배 연하가 된다. 아버지는 무엇을 하고 있는가?

[풀이]
아들을 만들고 있다(응?)
어머니를 Y, 아들을 X라 놓고 식을 만들면 Y=X+21
6년 안에 아들이 어머니 나이보다 5배 연하가 된다고 했으므로 X+21+6 = 5(X+6) 이 식을 풀어보면 X = -3/4, 즉 아들의 나이는 -3/4살,
즉 -9달이다. 아들이 태어나기 9달 전이라는 말로, 이 때 아버지는 어머니와 아기를 만들고 있었다.

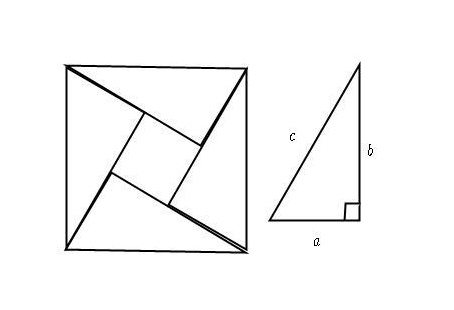
그리고 배 이름이 왜 하필 피타고라스인가 하니…
페르마의 밀실의 구조가 피타고라스 정리를 증명하는 그림과 똑같기때문에 배이름이 피타고라스라고 한다..

마지막에 인상깊었던 한마디…

세상은 그대로야

참고 : http://blog.naver.com/kyung6687?Redirect=Log&logNo=60120384786